Analysis of Mathematical Models for Neuronal Spiking
Mathematical modeling of electrophysiological phenomena and neural spikes using Hodgkin-Huxley and Van der Pol oscillator models
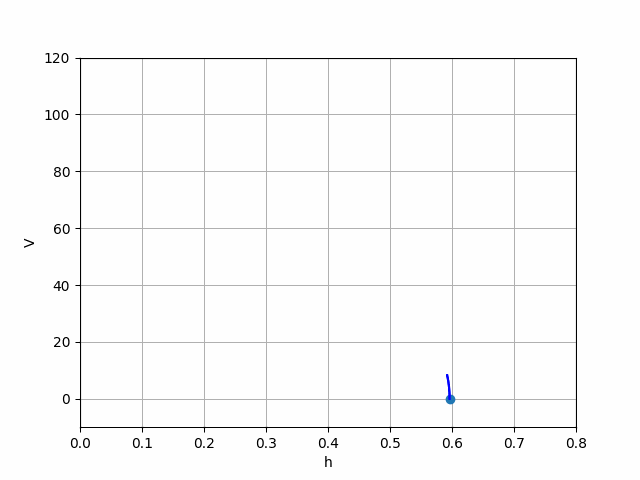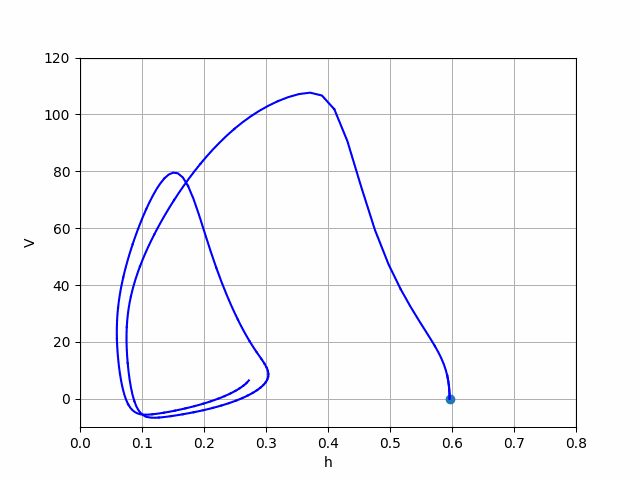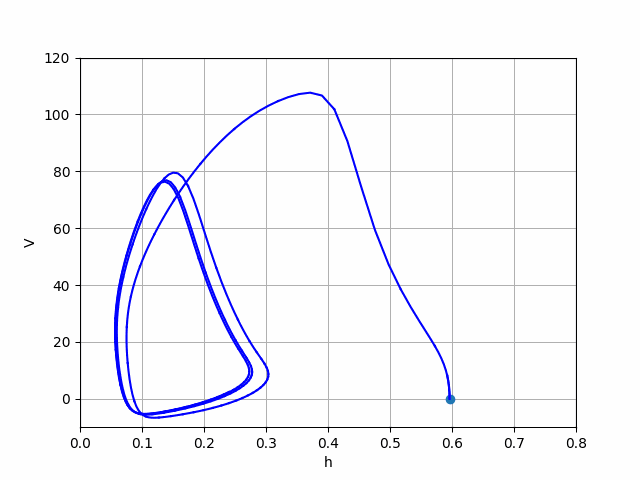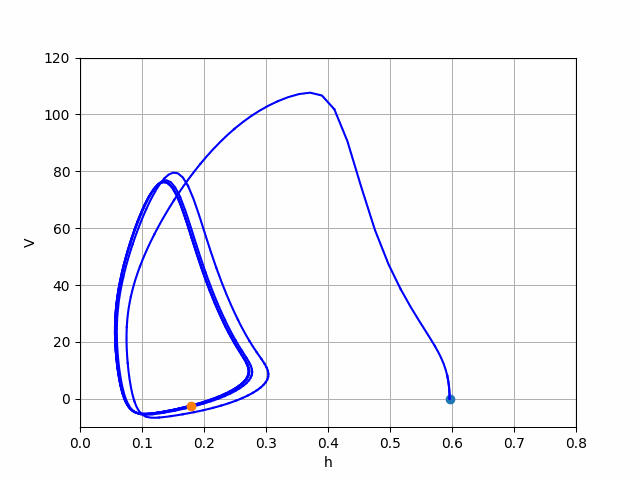
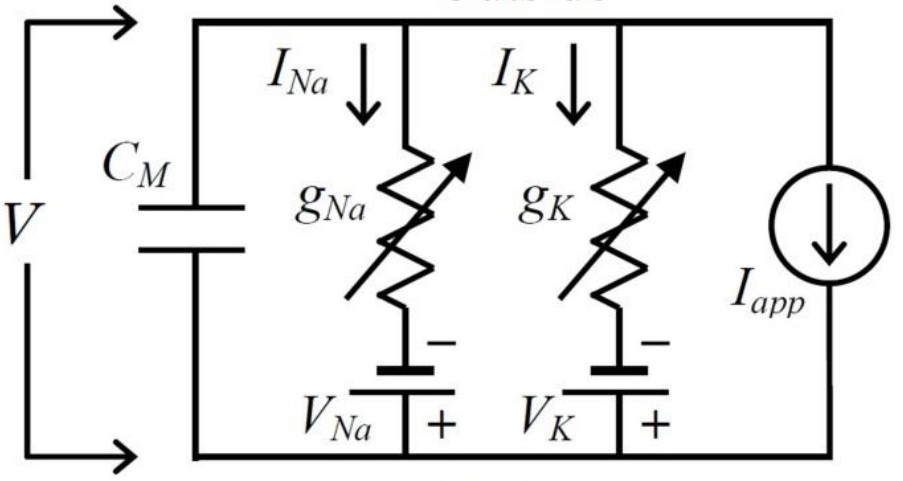
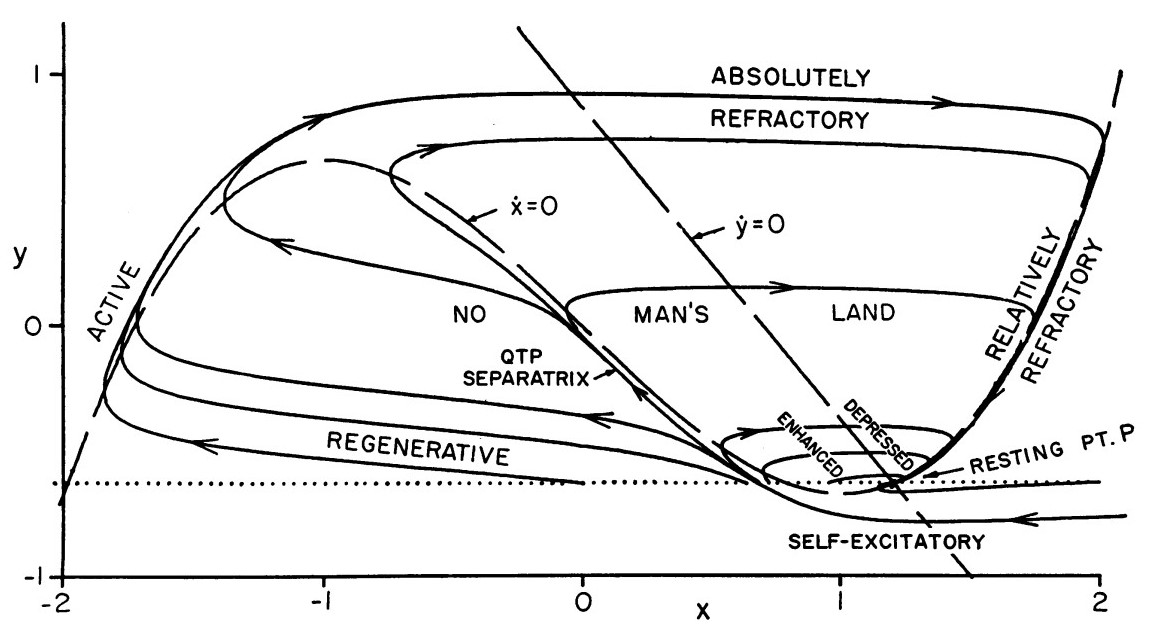
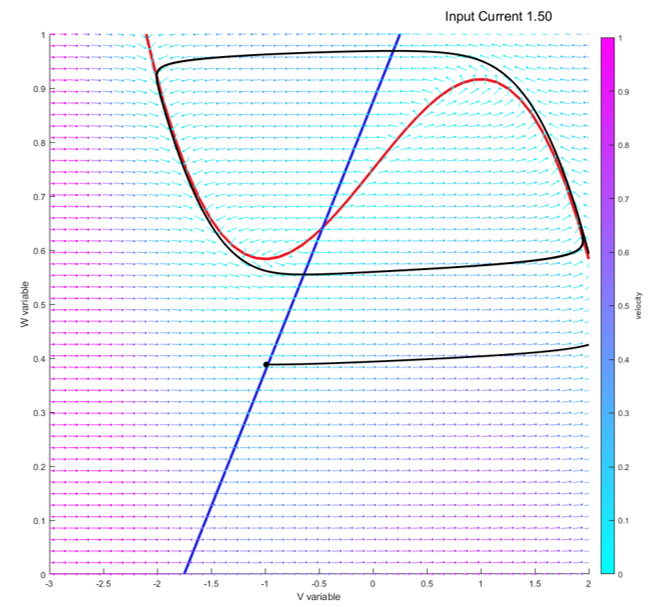
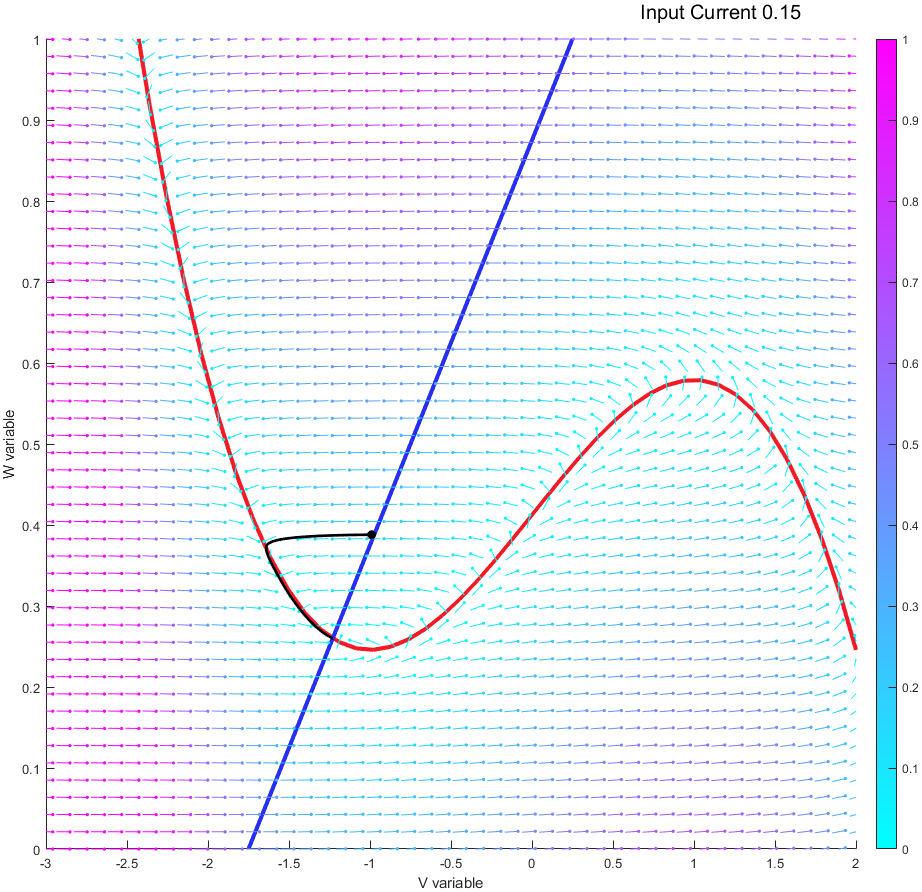
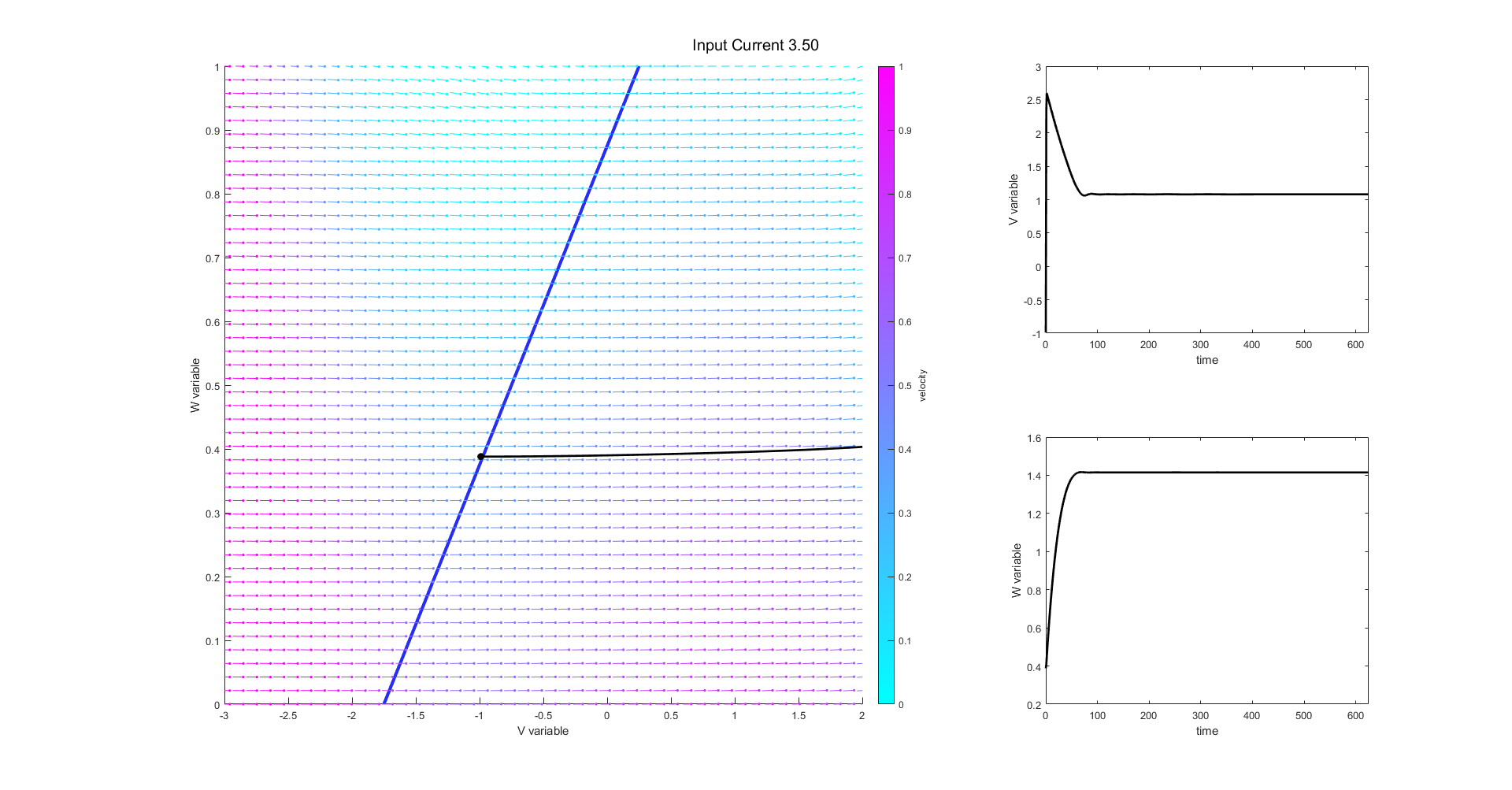
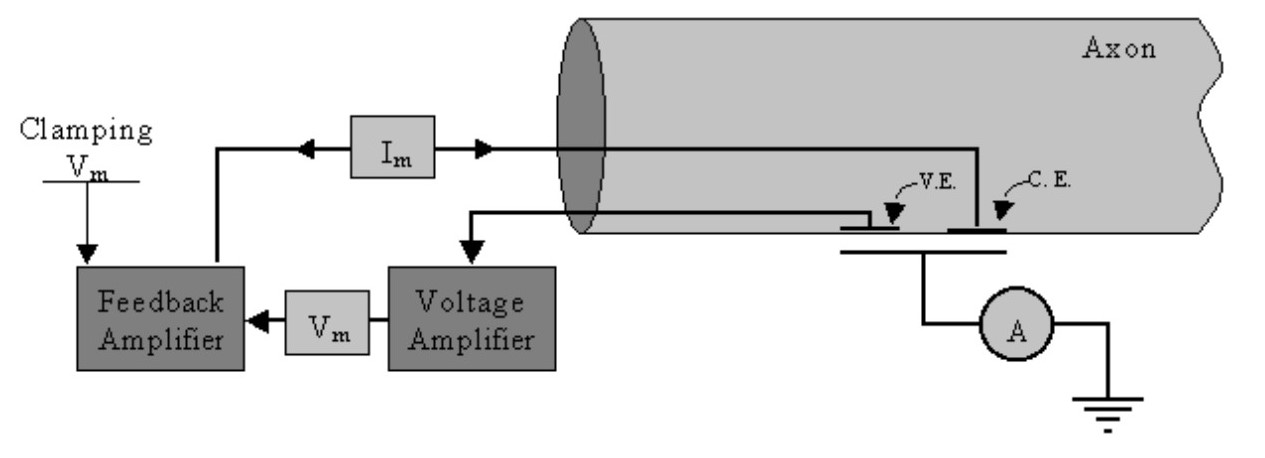
This work is focused on the mathematical models of the electrophysiological phenomena known as neural spikes. The need for accurate models of action potentials is shown along with the step by step formulation of the state of the art Hodgkin-Huxley (HH) model. Starting from the basic principles of entropy and diffusion the case for a more empirically based model is made. The formal assumption of the HH model are stated alongside the evidence of the model’s ability to fit real measurements. In addition, a simplified 2D model based on the Van der Pol oscillator is discussed in detail. This theoretical foundation in followed by numerical investigations of both models.
Technologies Used: Python, MATLAB, LaTeX
Project Link: Research Paper